Brain Teasers Riddles Elevator Game Rebus Puzzles
Puzzles and Brain Teasers
Brain teasers and puzzles help you to train your brain. So go ahead, take our Brain Teaser. And don't take a peek at the answer until you have tried really hard.Brain Teasers and Puzzles
In an interview for a Business school entrance exam the interviewer told the candidate "You have the option to choose between one tough question and 20 easy ones. Make your pick." Ben smartly answered, "I would go for the tough one." On his response the examiner asked him "What came first -- the hen or the egg?" Ben was nonplussed for a moment, but after a while firmly replied "The egg". On this the examiner with piqued interest asked "Why so?"
Can you tell us Ben's reply, as his answer impressed the examiner and he was selected for admission to that Business school?
Answer 
Ben's reply to the examiner was "The deal was just for one tough question!"
In an 800 m marathon, Steve managed to overtake his friend, Roderick, in the last 7 seconds of the race, who would have otherwise finished second.
- What place did Steve achieve after overtaking his friend?
- What place would Steve have achieved had he managed to overtake the last runner?
Answer
- Steve stood second by overtaking the second runner and not first which is a common mistake made by most of us.
- How can one overtake the last runner?
A train is scheduled from Amsterdam to New York (say Train A) and another from New York to Amsterdam (say Train B). The distance between the two stations is 3500 miles. At 14:00 hrs Train A leaves Amsterdam at a constant speed of 50 miles/hr. Two hrs later Train B leaves New York at a constant speed of 80 miles/hr. Each train makes a halt for 20 min at a station 20 miles from its starting point. Which train is nearer to New York when they meet?
Answer
Both the trains are equidistant from New York at the meeting point. The distance of the meeting point from New York will obviously be the same for both trains.
Nancy likes fresh flowers. Hence her husband got her some flowers. She found that if she put one flower per vase in her house, she had one flower left. But if she put two flowers per vase, she had one vase empty. How many flowers and vases did Nancy have?
Answer
Nancy had 4 flowers and 3 vases.
Let x be the number of flowers, and y be the number of vases.
x - y = 1
or
y = x - 1
From the statement "if she put two flowers per vase, she had one vase empty", we get:
2 (y - 1) = x
or
2 (x - 1 - 1) = x (putting the value of y from equation 1)
or
2x - 2 - 2 = x
or
2x - x = 4
or
x = 4
Hence, y = 3
Thus, Nancy had 4 flowers and 3 vases.
You are in a summer camp. As part of a team event you have to reach the top of the tree house at night and send a signal to your teammates. On reaching the tree top you find there a match, kerosene lamp, an oil burner, and a wood burning stove. Which would you light first?
Answer
The match.
Without lighting the match you cannot light any of the others.
It's Christmas time. Rachel has to decorate the Christmas tree with colorful lights. Her husband had packed these away in boxes last Christmas. One box has red lights, one box has blue, and one box has both red and blue. However, in the hurry to pack, her husband had labeled all the boxes wrongly. How can Rachel find out what each box contains by drawing just one light from one box?
Answer
Rachel takes one light out from the box which is labeled 'Blue and Red'. If it is a blue light, then this is the box which contains only blue lights, since the only other box that can contain blue lights is the one which has both blue and red lights. However, this cannot be that box since it already had the label 'Blue and Red' which we know is incorrect.
This means that the box marked 'Blue' actually contains red balls. This is because the only other box that remains is already marked 'Red' which we know is incorrect. This also means that the box marked 'Red' would contain both blue and red balls.
Had Rachel picked out a red light from the first box, then similar reasoning would lead us to the correct results.
Mrs. Benette was a school teacher who noticed that she took the same time to go to school in the morning as she took on her return journey from school back home, in the evening. One day she happened to discover something.
When she left home, the hour hand and the minute hand were cast exactly opposite each other and on reaching school she found them to be together.
Similarly, when she quit school in the evening, the hour hand and the minute hand were together and the moment she arrived home, they were exactly opposite each other.
How much time did Mrs. Benette spend traveling? Give the minimal possible answer.
Answer
1 hr, 5 mins and 27.2 secs.
The minute hand and the hour hand are together 11 times, in twelve hours,. It means that after every 12/11 hours, both the hands are together.
Similarly, the minute hand and the hour hand are exactly opposite to each other 11 times, in twelve hours. It means that after every 12/11 hours, both the hands are opposite each other.We know that at 12:00 both the hands are together and at 6:00 both the hands are exactly opposite to each other.
After 6:00, both the hands are in opposition at [6+(12/11)] hours, [6+2*(12/11)] hours, [6+3*(12/11)] hours and so on. The sixth such time is [6+6*(12/11)] hours, which is the first time after 12:00. Thus after 12:00, both the hands are opposite to each other at 12:32:43.6.
Hence, Mrs. Benette takes 32 minutes and 43.6 seconds to reach home from school. Her total travel time is twice of this time, which equals to 1hr, 5mins and 27.2 secs.
A wildlife photographer along with his driver was moving through an African jungle in his jeep. The jungle was dense and the road bumpy. The jeep accidentally hit a rock and the two men were thrown from their seats. The photographer's digital watch fell from his breast pocket and its battery popped out. Neither of them knew the correct time to re-synchronize the watch.
Thus the photographer asked his driver to visit the nearest forest officer's home and inquire the time. The driver drove the jeep at a constant speed to the forest officer's place, asked him the time, rested there for 5 mins and drove back to the jungle at the same speed at which he had gone. On the driver's arrival the photographer could set the right time on his watch. Can you tell me how?
Note - The driver did not have his own watch and neither did the forest office have a spare one which he could lend to the driver to take back with him.
Answer
Assume that when the driver left, the photographer had tuned his watch to a random time of 12:00 hrs.
Let the total travel time of the driver be 2t, as he drove with the same speed on his forward and backward journey.
On the driver's return, the photographer's watch read (12 + 5/60 + 2t). From this he could find out the value of t. The driver's journey from the time he quit the forest officer's home was T+t ( T being the time the driver noted while setting back for the jungle from the forest officer.) Since both the quantities are known the correct time could be determined.
At the grand ball dance thrown by the king, on the eve of the prince's wedding, each guest was asked to dance with any other partner, excluding his/her spouse. The pair could be formed between a man and a man, woman and a woman, man and a woman amongst the 20 couples who were invitees to the function and no partner could be repeated. At the end of the dance, the King was very curious to know the number of people, each invitee had danced with. So he asked everyone, to say aloud the number of people he/she had danced with and received 39 distinct replies. Mr. Beckham said he had danced with 38 people. Can you tell me how many people did Mrs. Beckham dance with?
Answer
Mrs. Beckham had danced with 0 person.
20 couples implied 40 people at the ball. No one was allowed to dance with his/her own spouse. No person danced with himself/herself or his/her spouse. Thus the maximum number of persons he/she could dance with is 40-2 = 38.
The problem says this person is Mr. Beckham. 39 distinct replies means 0,1,2,3,4.....38, plus one number that lies within this range. Since there are only 38 other invitees apart from Mr. Beckham and his wife, each one of the rest must have danced with at least one person. This leaves only the number '0', which is the number of person Mrs. Beckham danced with.
One evening you are sitting in a room with no windows and the door shut. Suddenly you hear two cars drive up outside. From the noise of the engines you can make out that one car's engine is well tuned, whereas the other car's engine is in urgent need of repair. The engines are switched off and you are asked to go out and identify the car with the good engine. You are allowed to start only one engine to hear the noise. However, when you get outside, you find 3 cars. You are told that one of them was already there for a long time. How can you be sure to find the car with the good engine?
Answer
The engines of the two cars which just arrived would be a lot warmer than the one which had been there for a long time. Hence I simply touch the hood of the cars and identify the two which just arrived. I then sit in any one and start the engine. If the noise is of the engine needing urgent repair then the car with the good engine is the other warm car. If not, then I am sitting in the car with the good engine.
An old lady had packed all her jewels in one box and wanted to send it to her grand-daughter. The lady possessed many locks and their keys but her grand-daughter had no copies of the keys. Although the jewel-box had facility for multiple locks, she could not parcel the key(s) to her grand-daughter for fear of it being intercepted. How could the lady send her jewels securely to her grand-daughter?
Answer
The lady would first lock the box with her own lock and send it to her grand-daughter without any key. The grand-daughter could then fix one of her own locks, whose key she possessed, onto the box and mail it back to her grand-mother. The lady would then remove her own lock and send the box back to her grand-daughter. The grand-daughter could then unlock her own lock and receive the jewels.
During the screening test for enrollment in an MBA program, each of the short-listed candidates had to individually face the following exam in order to qualify for the next round.
There were two rooms, one of which had 100 light bulbs, and the other contained their corresponding switches. Which switch belonged to which bulb was not known. The candidates were told that out of the 100 bulbs, 30 of them were glowing, while the rest were not. There was no way to tell whether the switches were in 'on' or 'off' state by just looking at them. A candidate was allowed to move between the rooms but could not see one room from the other. He was required to divide the switches into 2 groups such that each of them contained equal number of corresponding lighted bulbs. Toggling the switches would change the state of the corresponding bulb.
Could you help them devise a strategy?
Answer
A candidate would have to select 30 switches randomly from the collection and name it Group 1. Assume it had 'z' number of 'on' bulbs. Now the remaining switches which formed Group 2 had (30 - z) number of 'on' bulbs, since z + (30 - z) = 30. Now if he flipped all the switches of Group 1, the number of lighted bulbs would become (30 - z), which would be the same as the number of lighted bulbs in Group 2, i.e (30 - z).
A thief was caught and sentenced to death by the king. However, as a tradition of the land, each criminal could choose the way he would like to kiss death. But this thief was very cunning, can you tell me, what did he choose?
Answer
The thief chose natural death.
At a game show, George was given 3 wax sticks with a wick running along its length, each of which would take 2 hrs to burn, if lit at one end. The sticks were uneven in dimension (that is thicker at some places compared to the rest of the rope), hence if you cut the stick into two equal pieces you cannot assume that it would take one hour for them to burn.
George was told to use the sticks to measure 2½ hours. What did he do?
Answer
Firstly, he set fire to both ends of the first stick, which took an hour to burn (as it was burning with twice the rate.) [Count 1 hour].
As soon as it finished burning, he set fire to both ends of the second stick and one end of the third stick simultaneously; the second stick took another one hour to burn [Count 2 hours].
As soon as the second stick has burned off, George lit the other end too, of the third stick. As this stick had already burned for one hour already, with one hour remaining, it took half an hour to burn the remaining half. [Count 2½ hours.]
An affluent landlord needed to pay his gardener for revamping his garden, which would demand a week's hard work. But as he was short of cash, he decided that he would pay the gardener one ring each day, from a 7 link long gold chain that he possessed.
But the landlord did not want to make too many cuts in the chain as he wanted it back, once he had the cash to pay the gardener. What is the minimum number of cuts that the landlord needs to make in his chain?
Answer
The landlord needs to make only one cut on the third link, setting it free from both sides of the adjoining parts of the chain. This would result in 3 pieces:
1. 1 link (that was cut.)
2. 2 links joined together and
3. 4 links joined together.
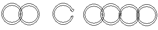
Day1. Give the single cut link.
Day2. Give the piece with 2 links and take back previous day's link.
Day3. Give the single link.
Day4. Give the piece with four links and take back the pieces with 1 and 2 links.
Day5. Give the single link.
Day6. Give the piece with 2 links and take back the single link.
Day7. Give the single link.
You have four 9's and you may use any of the following operations (+, -, /, *) as many times as you like. You have to create a mathematical expression which uses exactly four 9's to give a result of 100.
How many such expressions can you make and what are they?
Answer
There are 5 such expressions:
99 + (9/9) = 100
(99/.99) = 100
(9/.9) X (9/.9) = 100
((9*9) + 9)/.9 = 100
(99-9)/.9 = 100
At a conference, 12 members shook hands with each other before & after the meeting. How many total number of hand shakes occurred?
Answer
132
The first person shook hands with 11 remaining people, the second person also shook hands with 11 people, but we count 10, as the hand shake with the first person has already been counted. Then add 9 for the third person, 8 for the fourth one & proceeding in this fashion we get:
11 + 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 66
66 hand shakes took place before & 66 after the meeting, for a total of 132.
A milkman has a can of 20 gallons, full of milk. But due to a sudden epidemic, all his cows in the farm fall sick. He can no longer collect milk from them.
To conserve his milk he decides that on the first day he will sell one liter and refill the can back with water. On the 2nd day he will take out 2 liters and refill the bottle. On the 3rd day he will take out 3liters and so on...
By the time all the milk is gone, how much water has the milkman sold?
Answer
The milkman has sold 190 liters of water.
It is given that the milkman had a 20 liters can of milk. From the first day, when he sold 1 liter of milk, until the end of 20 days, he must have sold
(1 + 2 + 3 + 4 + ..... +18 + 19 + 20) = 210 liters of adulterated milk.
Out of that 210 liters, 20 liters was pure milk which he had initially. Hence, he must have sold
(210 - 20) = 190 liters of water.
A safe of a treasure chest can be unlocked with a 5 digit key. The following is known about it. The 4th digit is 4 greater than the second digit, while the 3rd digit is 3 less than the 2nd digit. The 1st digit is thrice the last digit. There are 3 pairs whose sum is 11. Find the number.
Answer
65292
As per given conditions, there are three possible combinations for 2nd, 3rd and 4th digits. They are:
3, 0, 7 or
4, 1, 8 or
5, 2, 9
It is given that there are 3 pairs whose sum is 11. All possible pairs are
2, 9
3, 8
4, 7
5, 6
Now required number is 5 digit number and it contains 3 pairs of 11. So it must not be having 0 and 1 in it.
Hence, the only possible combination for 2nd, 3rd and 4th digits is
5, 2, 9
Also, the 1st digit is thrice the last digit. The possible combinations are
3, 1
6, 2
9, 3
Out of these only (6, 2) with (5, 2, 9) gives 3 pairs of 11. Hence, the answer is 65292.
Out of the 70 employees working with ABC Inc., 30 are females. Also,
- 30 employees received a promotion
- 24 employees are above 30 years of age
- 19, amongst the promoted employees are over 30 years, of which 7 are males
- 12 males are above 30 years of age
- 15 males have received a promotion
Answer
15 un-promoted females & none are above 30 years of age.
Simply putting all given information into the table structure, we get the answer.
As per the will of a late farmer, his property would have to be divided in the following way. The eldest got half of the land and an added 2 acres. Second son received of the remaining land plus 2 acres. Third son got half of the remaining +2 acres. But as the fourth son took half of the remaining plus 2 acres of land, there was nothing left for the fifth son. How many acres of land did the farmer originally have?
Answer
The farmer originally owned 60 acres of land.
Let the original amount of land be x acres.
1st son got x⁄2 +2 = (x+4)⁄2
Land remaining = x - (x+4)⁄2 = (x-4)⁄2
2nd son got {(x+4)⁄4 + 2}
Proceeding like this, what remain after 4th son gets his share is (x-60)⁄16
This obviously equates to 0, as there is nothing left for 5th son.
x - 60 = 0
Hence, x = 60
Ms. Janette takes a train to her granny's place. While on her journey she falls asleep when the train still has twice as far to go as it has already gone.
Halfway through the trip she wakes up when the train stops at a signal. When she finally falls asleep again, the train has yet half the distance to go that it has already traveled. Fortunately, Ms. Janette wakes up at the end of her trip.
What fraction of the total trip did Ms. Janette travel sleeping?
Answer
Ms. Janette slept through half her trip.
Let's draw a timeline. Picture the train route on a line shown below:
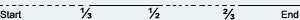
----- shows time for which Ms. Janette was not sleeping
___shows time for which Ms. Janette was sleeping
Adding up, all sleeping times,
= (½ - ⅓) + (1 - ⅔)
= ⅙ + ⅓
= ½
The workforce of a firm is divided into 4 groups for allocation to different projects. Each group is a motley of Managers, Technicians and Executives.
- Group I : 1 Manager, 1 Technician and 1 Executive
- Group II : 1 Manager, 5 Technicians and 7 Executives
- Group III : 1 Manager, 7 Technicians and 10 Executives
- Group IV : 9 Managers, 23 Technicians and 30 Executives
The cumulative wage of all the members of Group II costs $300 and that of Group III members costs $390. Can you calculate, what wage expense the Company bears for Group I and Group IV members?
Answer
Group I wage is $120 and Group IV wage is $1710
Assume that the wages of a managers, a technician and an executive are M,T and E respectively.
For Group II : M + 5T + 7E = 300 .....(i)
For Group III : M + 7T + 10E = 390...(ii)
Subtracting equation (ii) from (i) : 2T + 3B = 90
For Group I:
= M + T + B
= (M + 5T + 7E) - (4T + 6E)
= (M + 5T + 7E) - 2(2T + 3E)
= 300 - 2(90)
= 300 - 180
= 120
Similarly, for Group IV:
= 9M + 23T + 30E
= 9(M + 5T + 7E) - (22T + 33E)
= 9(M + 5T + 7 E) - 11(2T + 3E)
= 9(300) - 11(90)
= 2700 - 990
= 1710
A beautiful lake was surrounded by 4 churches. When flowers are washed in the lake-water, the flowers doubled in number. On Easter day, Mrs. Benette went there with some Easter Lilies. She washed the lilies in the lake-water before entering each church. In each of the church she deposited the same number of flowers. By the time she was done with all the four churches, she had no flower left with her.
- How many flowers did she deposit in each church?
- What is the least number of flowers Mrs. Benette must have had initially to make the above possible?
Answer
Mrs. Benette deposited 16 Easter Lilies at each church and she had originally brought 15 of them.
Lets say Mrs. Bennette had x flowers with her initially.
When she washed them in the lake, they doubled in no. hence she had 2x flowers.
She deposited y (say) flowers in the first church and came out with 2x-y flowers.
She washed them in the lake waters and had 2(2x - y) flowers.
She entered 2nd church with 2(2x - y) flowers = 4x - 2y
She came out with (4x - 2y ) - y flowers = 4x - 3y
She entered 3rd church with 2(4x - 3y) flowers = 8x - 6y
She came out with (8x - 6y)- y flowers = 8x - 7y
She entered 4th church with 2(8x - 7y) flowers = 16x - 14y
And deposited all of them there, hence
16x - 14y = y
Or, 16x =15y
Since we are interested in the least possible x,
x=15
y=16
On a stormy night torn with torrential rain, I crossed a bus-stand where three people were waiting. One amongst them, I recognized as my bosom friend, who had once saved my life so I owed him something. Second was an old dying lady, who needed urgent medical attention, and last but not the least, was the person of my dreams, someone whom I would propose for marriage. But the snag was that I was driving a 2-seated car, and had room left for only one person. Yet I managed to salvage the situation.
How?
Answer
Quite simple. I got down from my car, and handed the keys to my friend, asking him to drive the old lady to the hospital; while I waited with the girl of my dreams for the bus.
In the city of Wonderland, the following facts are true:
- No two residents have exactly the same income.
- No resident's income exactly amounts to $3055.
- The number of residents outnumbers the income of individual residents.
What is the largest possible population strength of the city of Wonderland?
Answer
3055.
It is given that no resident's income exactly amounts to $3055.
Hence there are 3055 residents with their income ranging from $0 to $3054. Assuming more than 3055 residents will violate the 3rd condition.
As for any number exceeding 3055, there will be same number of residents as the income of highest earning resident.
In a Derby race, Bambino, Pascoe, Lexus and Jackie are taking part. Three bidders Antonio, Harry, James made the following statements regarding results.
The following information about their choice was supplied:
- Antonio said either Bambino or Jackie will definitely win.
- Harry said he is confident that Bambino will not win.
- James said he is confident that neither Jackie nor Lexus will win.
When the results were out, it was found that only one of the above three had made a correct statement. Can you tell who has made the correct statement and who has won the contest?
Answer
Harry; Lexus.
If Antonio is correct, then either of Harry or James will be correct depending on whether Bambino or Jackie win the race. This directly contradicts the given argument that only one of the bidder's statements is true. Similar is the case with James.
However if Harry's statement is held true, then, both Antonio and James's statements will automatically be false, if we reason out the winner to be Lexus.
Four travelers are parting ways on a four head crossing. The travelers, Mr. East, Mr. West, Mr. South and Mr. North head towards different directions after parting.
The following information about their choice was supplied:
- The routes were The North Road, South Road, East Road and West Road.
- None of the travelers took the road which was their namesake.
- Mr. East did not take the South Road.
- Mr. West did not the South Road.
- The West Road was not taken by Mr. East.
Can you tell which road did each traveler take?
Answer
- Since Mr. East cannot take South Road and West Road (given) and East Road (because it is his namesake), he obviously chose the North Road.
- Mr. West did not take the South Road (given) and not the West Road (because it is his namesake) hence he must have taken the East Road.
- Mr. West did not take the South Road (because it is his namesake), hence he must have taken West Road.
- Finally, we are left with Mr. North who must have taken the South Road.
Three friends namely George, Michael and Robert are friends.
- George is a widower and lives alone with his only daughter who takes care of him.
- Michael is a bachelor and his niece cooks for him and looks after his house.
- Robert is married to a charming lady called Christina and they live together in a large apartment in the same town.
Christina suggests that all of them could stay together in a single house and share monthly expenses equally. During their first month of living together, each person contributed $1025. At the end of the month, it was found that $4068 was the total expense so the remaining amount was distributed equally among everyone. The distribution was such that everyone received $8 each. How do you explain the situation?
Answer
George's daughter, Michael's niece and Robert's wife are one and the same person - Christina.
According to the problem,
Total contribution = 1025 x 4 = $4100
Total expenditure = $4068
Therefore amount remaining = $4100 - $4068= $32
Each person received $8
Hence there are $32/$8 = 4 persons
They are:
- George
- Michael
- Robert
- Christina
500 potted plants were grown in a nursery. Some of them were tall, while others were of the dwarf variety. They were arranged in an array of 10 rows and 50 columns according to their height.
The pots of the tallest plants among each row of all are painted pink. And the shortest among them is painted red.
Similarly, the pots of the shortest plants among each column are painted yellow. And the tallest amongst them is painted orange.
Now can you tell which pot has the taller plant, the red pot or the orange one?
Answer
In both the situations, plant X501 satisfies the condition. Thus the red and orange painted pots actually refer to the same plant.
As per the puzzle, 500 plants were arranged in order of their height (say, ascending order of their height). Diagrammatically, it can be represented as:
X1010.......................X5010
X99...........................X509
X88...........................X508
.
.
.
.
X11.......................X501
The plant positioned in the last position of the last column (X5010) is the tallest amongst all plants and the plant posted on the first position of the first column (X11)is the shortest amongst all.